The Notorious Prime Numbers
Date: 2021-05-11
Haunting Mathematicians since forever!
I have heard of advanced mathematical concepts like Analytical Continuation, Statistical Inference and so on… but do you know that the mysteries of one of the oldest concepts of mathematics… The Prime Numbers, are yet to be discovered!!
To discover more about prime numbers, let us go back to 323 BC, and when its this old, we know its Euclid of Alexandria, the father of geometry himself!!
Mr.Euclid apparently wrote a mathematical treatise of 13 books which have never been out of print since the printing press was invented. The mathematical and logical rigour of this book is so high, that it wasn’t matched till the 19th century.
 Title page of Sir Henry Billingsley first English version of Euclid’s Elements, 1570
Title page of Sir Henry Billingsley first English version of Euclid’s Elements, 1570
Second only to the Bible in the number of copies printed, this book contains proofs to the most profound problems in number theory and geometry.
One such proof suggests that there are infinitely many prime numbers.
How? I’ll try to phrase it,
To prove that there are infinitely many prime numbers, assume that there are only a finite number of prime numbers and that they are on the following set.
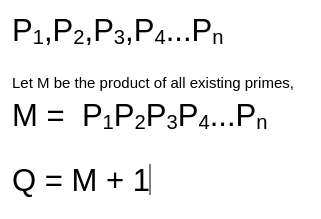
If Q is prime, then there exists at least one more prime that is not on the list, and hence there is a contradiction and therefore there are an infinite number of prime numbers.
If Q is non-prime, then there must exist a prime number “p” on the list of prime numbers we initially considered, such that p divides Q.
We now know that,
p divides Q and p also divides M (since M is the product of all prime numbers)
since, Q = M+1,
p must also divide the difference of Q and M, i.e, 1.
Since there is no prime number that can divide 1, p does not exist in the list and is a prime. Which means there is at least one more prime that is not on the list we considered.
Example 1,
Consider that there are only 4 primes,
2,3,5,7
M = 235*7 = 210
Q = 211
But, 211 is a prime number.
Example 2,
Consider that our list of primes is,
2,3,5,7,11,13
M = 235711*13 = 30030
Q = 30031 = 59*509
but, 59 is a prime that is not on the list of all primes that we considered!
Hence the proof!
To put it simply, the appearance of these prime numbers, on the number line, the pin point distribution of these prime numbers is yet to be found, the largest prime number we know for now is 2⁸²⁵⁸⁹⁹³³ -1, but there is no way as of now to predict a prime number. We do have very strong theorems, which are waiting to be proven.
And hence the stage is set for a long and confusing history of prime numbers, little is known about this wonderful series of excellence, which has been far from the reach of humanity’s grand mathematicians. After Euclid, many tried to tame the primes. Not one could succeed, but every single time we struck hard enough, we got close… now, all that we require is a proof, for the Riemann Hypothesis.
What is the Riemann Hypothesis?
So, basically Riemann Hypothesis, is a millennial problem, one of many proposed by the Clay Mathematics Institute on May 24, 2000. Its been almost 21 years and as of now, only 1 problem has been solved. Solving these problems earns you a million dollars, but that is trivial as opposed to a seat in the Hall of Fame of Mathematics.
*Poincare conjecture* *P versus NP* *Hodge conjecture* *Riemann hypothesis* *Yang–Mills existence and mass gap* *Navier–Stokes existence and smoothness* *Birch and Swinnerton-Dyer conjecture*
Only one has been solved as of now, that is the Poincare conjecture.
An Interesting Story about the Poincare conjecture :
After a century’s effort by mathematicians around the world, a random mathematician, who the world didn’t know much posted a paper on arXiv and the paper was floating around the internet for a while until one morning…
After a team of mathematicians found the paper on the internet, they were shell-shocked. He used “Ricci Flow”, which was a program derived from a failed attempt of Richard S Hamilton in cracking the Poincare conjecture.
The man’s name was later revealed to be Grigori Yakovlevich Perelman. He was offered the 1 million dollars by the Clay Institute, which he…DECLINED!! , since he thought Richard S Hamilton was equally creditable for the proof.
He was also offered the Fields Medal, for his contributions to geometry and his revolutionary insights into the analytical and geometric structure of the Ricci flow, which he again declined.
“I’m not interested in money or fame; I don’t want to be on display like an animal in a zoo.”
Several teams of mathematicians came together and checked if he was right about the proof, which he was.
Such is the greatness of one of the greatest problems to be solved. Now you know what you are dealing with.
I won’t add his photo since he told me he doesn’t like fame…
Riemann Hypothesis and how it came about has a long history, enough for me to write a separate story about it.
